Introduction
参加了一下密码挑战赛。
题目是(低汉明重量)子集和问题,我们做得还不错,一共9级挑战,解出了前8级。
思路:可以转化为求解SVP(CVP),然后用Lattice Reduction Algorithm来解。
- 比赛链接: http://cmsecc.com/
- our paper: https://mega.nz/file/CWgxXA7Y#GC0W9HTHnNmcHuKvPdnm4xQi3MQEptfha9le1V_r2F0
- source code: https://mega.nz/file/nSp3jQqI#2GMIeZx6hDLET2jrw9gWYaaa_F3dCZg-Hv2TN1rX6F8
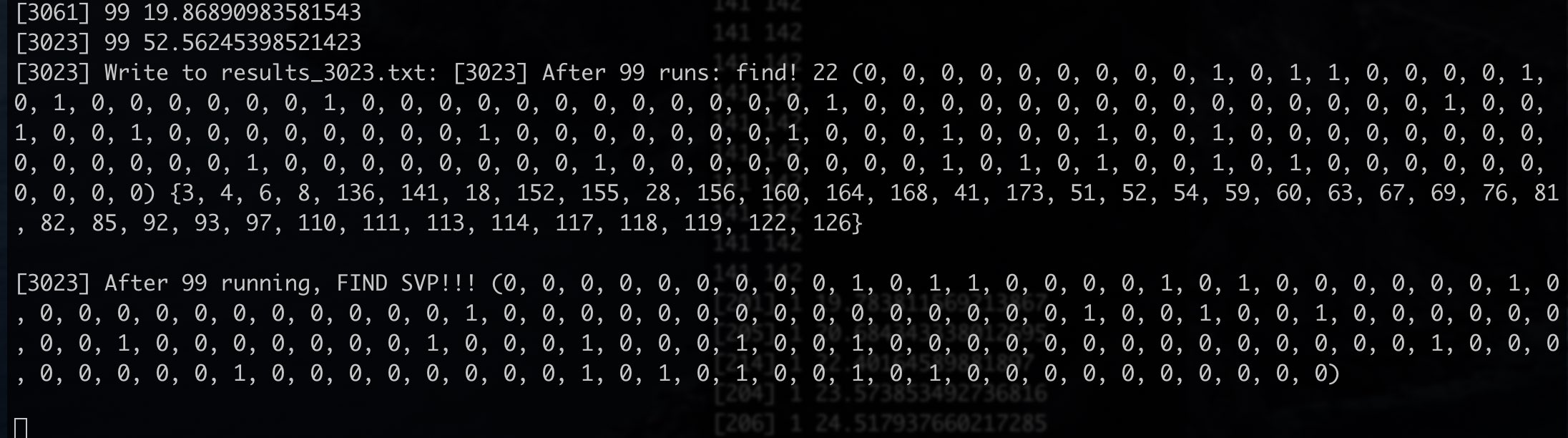
跑出来180维的截图纪念:
Timeline
看了一些相关的远古paper,记录了一下大概的发展过程。(只是找了一些,不是很全,还有很多)
1976 Diffiem, Hellan在New directions in cryptography中提出了Public Key Cryptography和Digital Signature的概念(但没有给出一个具体的方案,只有一个用于密钥交换的Diffie-Hellman Key Exchange)
早期最有名的两个PKC:
-
RSA
A method for obtaining digital signatures and public-key cryptosystems
-
Merkle-Hellman
Hiding information and signatures in trapdoor knapsacks
(在这里,knapsack 约等于 subset-sum,实际上后者是前者的一个特例情况)
Cryptosystems Based on Subset-sum Problem
-
1978 Merkle-Hellman PKC
Hiding information and signatures in trapdoor knapsacks
-
1978 Graham-Shamir PKC
Cryptology in Transition
-
…
-
1988 Chor-Rivest PKC (高密度,以防止low-density attack)
A knapsack-type public key cryptosystem based on arithmetic in finite fields.
-
…
Cryptanalysis
-
1982 Shamir’s破解Merkle-Hellman PKC (single-iterated Merkle-Hellman)
A polynomial time algorithm for breaking the basic Merkle-Hellman cryptosystem
-
(1982 LLL algorithm横空出世。从此,关于子集和问题的cryptanalysis,大多都和lattice相关)
Factoring Polynomials with Rational Coefficients,
-
1982 Adleman(第一次)用LLL来解subset-sum problem
On breaking generalized knapsack publick key cryptosystems.
-
1984 Brickell用LLL来解low density knapsacks
Solving low density knapsacks.
-
1985 Brickell用LLL来解multiply-iterated Merkle Hellman(较复杂)
Breaking iterated knapsacks.
The cryptanalysis of Merkle-Hellman schemes was the first application of lattice reduction in cryptology
-
1985 Lagarias和Odlyzko用LLL来解low density subset-sum problems,d < 0.645(不是那么的复杂)
Solving low-density subset sum problems.
-
1986 …
On the Lagarias-Odlyzko algorithm for the subset sum problem.
-
1988 一篇survey
Cryptanalysis: A Survey of Recent Results
-
1990 一个关于subset-sum的survey
The rise and fall of knapsack cryptosystems.
-
1992 Coster等人进一步优化Lagarias和Odlyzko的结果(d < 0.9408)
Improved low-density subset sum algorithms.
-
1997 Vaudenay破解Chor-Rivest PKC
Cryptanalysis of the Chor-Rivest cryptosystem.
-
2001 Nguyen的一篇关于lattice in cryptology的总结
The Two Faces of Lattices in Cryptology
To summarize, the subset sum problem can always be efficiently reduced to CVP, and this reduction leads to an efficient probabilistic reduction to SVP in low density, and to a polynomial-time solution in extremely low density. In the light of recent results on the complexity of SVP, those reductions from knapsack to SVP may seem useless. Indeed, the NP-hardness of SVP under randomized reductions suggests that there is no polynomial-time algorithm that solves SVP. However, it turns out that in practice, one can hope that standard lattice reduction algorithms behave like SVP-oracles, up to reasonably high dimensions. Experiments carried out in [85,124,125] show the effectiveness of such an approach for solving low-density subset sums, up to n about the range of 100–200. It does not prove nor disprove that one can solve, in theory or in practice, low-density knapsacks with n over several hundreds. But it was sufficient to show that knapsack cryptography was impractical: indeed, the keysize of knapsack schemes grows in general at least quadratically with n, so that high values of n (as required by lattice attacks) are not practical. Thus, lattice methods to solve the subset sum problem are mainly heuristic. And lattice attacks against knapsack cryptosystems are somehow even more heuristic, because the reductions from knapsack to SVP assume a uniform distribution of the weights ai’s, which is in general not necessarily satisfied by knapsacks arising from cryptosystems.
Summary
还有很多不足的地方(还有很多可以进一步深入研究的空间):
-
BKZ算法可以用extreme pruning来优化
-
有比BKZ算法更好的求解SVP的方法(Sieving): https://www.latticechallenge.org/svp-challenge/halloffame.php
-
Zero-Forced那边预估的概率很有问题,不是很严谨(感觉概率论白学了)
-
Zero-Forced大概率是负优化,但应该有某个降维点可以达到最优,没去找
-
160维的BKZ应该能跑出来,不过挺费时间的,就没去测试。
-
感觉应该破费一下,把最后200维解出来的。但是又感觉不是很值得。。。(不会真有其他人能解出200维吧?)
-
第二章可以再多水点字的
-
有一个启发式解法: 基于联立丢番图逼近的子集和问题启发式求解算法
这个paper的作者大概率就是出题人了。稍微去试了一下,发现也并不是很容易,就没怎么深入研究了
-
一些国内的中文paper也没去找。不过感觉这种子集和问题真能有高效的求解算法,为什么不直接发顶会呢?