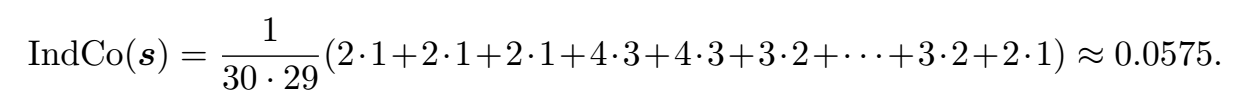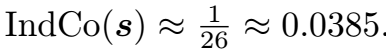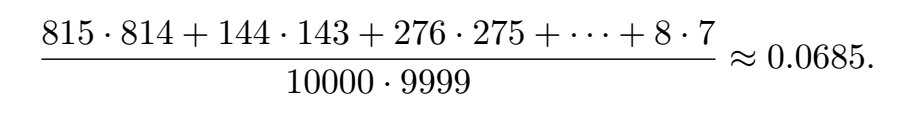在本文中,我们将先给出Vigenere Cipher的一个简单介绍以及加密和解密过程,然后利用一些数学方法对Vigenere Cipher进行密码分析,最后对两道相关的CTF题目进行讲解。
Vigenere Cipher是一个polyalphabetic cipher,多表替换密码。
源自于Blaise de Vigenere(1523-1596)在1586年写的一本叫做Traicte des Chiffres书中。
但并不是Vigenere他个人发明的。
Vigenere Cipher通过使用多个偏移量向右移位字母来加密。
使用一个keyword或者phrase来决定偏移量。
e.g.
明文:The rain in Spain stays mainly in the plain.
keyword:flamingo
P || t h e r a i n i | n s p a i n s t | a y s m a i n l | y i n t h e p l | a i n
K || f l a m i n g o | f l a m i n g o | f l a m i n g o | f l a m i n g o | f l a
C || y s e d i v t w | s d p m q a y h | f j s y i v t z | d t n f p r v z | f t n
得到密文:ysedivtwsdpmqayhfjsyivtzdtnfprvzftn
Note:Vigenere Cipher中,虽然同一个明文字母可以被加密成不同的密文字母,但是也有可能一段相同的明文部分,会被加密成相同的密文部分。例如,在rain和mainly中的ain都被ing加密成ivt。但也有被加密成不同的密文部分,明文末尾的ain就被加密为ftn。
解密的话,按照偏移量左移字母即可。
keyword长度问题:
长:较为安全
短:易于记忆、使用
Efficiency (and ease of use) <————– versus ————–> Security.
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
from itertools import cycle
from string import ascii_lowercase as alphabet
def Vigenere_enc(pt, k):
'''
Encryption of Vigenere Cipher.
:param str pt: The plaintext to be encrypted.
:param str k: The keyword to encrypt the plaintext.
:return: The ciphertext after encryption.
:rtype: str
'''
shifts = cycle(alphabet.index(c) for c in k)
ct = ''
for c in pt.lower():
if c not in alphabet: continue
ct += alphabet[(alphabet.index(c) + next(shifts)) % len(alphabet)]
return ct
def Vigenere_dec(ct, k):
'''
Decryption of Vigenere Cipher.
:param str ct: The ciphertext to be decrypted.
:param str k: The keyword to decrypt the ciphertext.
:return: The plaintext after decryption.
:rtype: str
'''
shifts = cycle(alphabet.index(c) for c in k)
pt = ''
for c in ct.lower():
if c not in alphabet: continue
pt += alphabet[(alphabet.index(c) - next(shifts)) % len(alphabet)]
return pt
|
测试效果:

在历史上很长一段时期内(16世纪~19世纪),Vigenere Cipher都是被认为是不可破的,事实上,时间会证明一切。
一般来说,破解Vigenere Cipher需要两步:确定密钥长度,恢复密钥。
首先,我们必须要确定出密钥长度,有两种方法:
- Kasiski Test
- The Index of Coincidence Test
这个方法是一个叫Friedrich Kasiski的德国军事官员在他的书Die Geheimschriften und die Dechiffrir-kunst (Cryptography and the Art of Decryption)中提到的。
思路:寻找密文序列中重复的片段,列出重复的片段之间相隔的距离,那么密钥长度很大概率上能够整除这些距离。
正如之前加密例子中一样:

密文序列中ivt出现了两次,相隔距离为16,密钥长度8能整除16。
Note:由于birthday paradox,在密文序列中寻找到重复片段的概率实际上要比我们想象的要高很多。
限于篇幅,不详细展开。感兴趣的可以去Vigenere Cipher - wiki
上看看。
假设Vigenere Cipher的密钥长度为 $k$ ,那么间距为 $k$ 的字母必然是由keyword中的同一个偏移量来加密的。
将密文字符串 $s$ 分成 $k$ 组
$$
s_1, s_2, …, s_k
$$
其中子字符串 $s_1$ 由从第一个字母开始每相隔距离为 $k$ 的字母组合而成, $s_2$ 由从第二个字母开始的每相隔 $k$ 个字母 组合而成,依次类推。
如果我们把 $s$ 写成
$$
s = c_1c_2c_3…c_n
$$
那么
$$
s_i = c_ic_{i+k}c_{i+2k}c_{i+3k}…
$$
且 $s_i$ 中的每一个字母都是用同一个偏移量加密而成的。
也就是说,Vigenere Cipher实际上就是多个不同偏移量的凯撒(移位)密码的组合。
凯撒密码是一种简单的单表替换密码,由于凯撒密码的密钥空间极小(仅有26种可能的密钥),仅凭暴力穷举即可破解;但另一方面,正因为凯撒密码是一种简单的替换密码,加密前后字母之间的频率分布规律不变,我们也可以用频率分析的方法来破解。
e.g.
将密文字符串 $s = \text{ysedivtwsdpmqayhfjsyivtzdtnfprvzftn}$ 分成8组:
$$
\begin{aligned}
s_1 &= \text{ysfdf}\
s_2 &= \text{sdjtt}\
s_3 &= \text{epsnn}\
&…\
s_8 &= \text{whzz}
\end{aligned}
$$
其中每一组都是用keyword中同一个对应字母的偏移量移位加密而成。
分组的关键是要找到密钥长度到底是多少。
我们可以一个一个地去猜测密钥长度,i.e.,k=2, 3, 4, ...。如果我们刚好猜中密钥长度,那么每一组子字符串 $s_i$ 的频率分布规律应当和普通的英文文本的分布规律相似的,会有一些字母像英文文本中字母e, t, a, o一样,出现的次数很多,也会有一些会像j, x, q, z一样,频率极低;如果没有猜对长度,那么每一组 $s_i$ 的频率分布规律应当就像随机选取一样,每一个字母的出现的次数都差不多。
问题是:我们如何区分这两种频率分布?
先给出index of coincidence的概念:
Definition. Let $s = c_1c_2c_3…c_n$ be a string of $n$ alphabetic characters. The index of coincidence of $s$, denoted by $\text{IndCo}(s)$, is the probability that two randomly chosen characters in the string $s$ are identical.
定义:令 $s$ 是一串长度为 $n$ 的字符串。那么,$s$ 的index of coincidence就是从字符串 $s$ 中随机选取出两个字符且这两个字符相同的概率,记作 $\text{IndCo}(s)$.
下面我们利用一些基本的排列组合和概率知识推导出index of coincidence的公式:
我们可以用数字 $0, 1, …, 25$ 来分别代表字母 $a, b, …, z.$
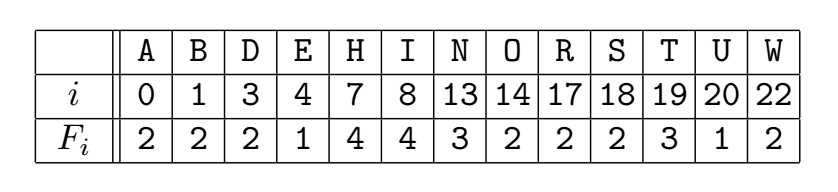
令 $F_i$ 表示字母 $l$ 在字符串 $s$ 中的频率。例如,字母 $h$ 在字符串 $s$ 中出现的次数是23,那么 $F_7 = 23$。(字母 $h$ 对应数字7)
对每一个 $i = 0, 1, …, 25$,都有 $\binom{F_i}{2} = \frac{F_i(F_i - 1)}{2}$ 种方法来从字符串 $s$ 中选出两次第 $i$ 个字母。
另一方面,总共有 $ \binom{n}{2} = \frac{n(n-1)}{2}$ 种方法从字符串 $s$ 中任选两个字母。
那么,任选两个字母,且选出的这两个字母相同的概率为:
$$
\text{IndCo}(s) = \frac{1}{n(n-1)} \sum_{i=0}^{25}F_i(F_i-1)
$$
e.g.
令 $s$ = “A bird in hand is worth two in the bush.”
忽略空格,$s$ 由30个字母构成。
代入推导出的公式中,得到$s$ 的index of coincidence为:
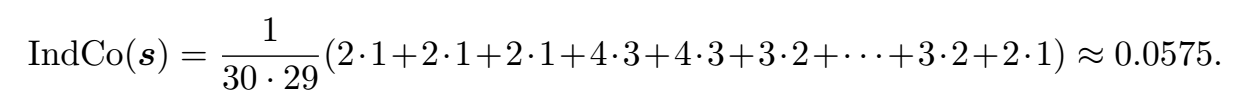
如果 $s$ 是从26个字母中随机选取的,即每个字母被选取的概率相同,为$\frac{1}{26}$,那么 $s$ 的index of coincidence大约为:
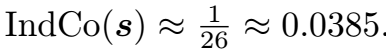
如果 $s$ 是英文文本,那么按照字母频率
,一个长为10000的字符串中大约有815个A,144个B,276个C,依次类推。
因此,正常英文文本的index of coincidence大约为:
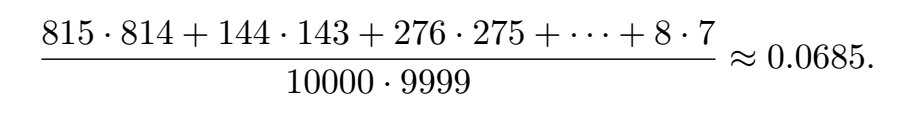
因此,可以先计算出 $s$ 的index of coincidence,然后根据结果和0.0385与0.0685之间的差距来判断 $s$ 是否是一段和普通的英文文本相似频率分布的字符串:
如果$\text{IndCo}(s) \approx 0.068$,那么 $s$ 很可能就是一段和普通英文文本相似频率分布的字符串;
如果$\text{IndCo}(s) \approx 0.038$,那么 $s$ 很可能就是一段随机的字符串。
$\text{IndCo}(s)$越大:越像是被某种简单替换加密的英文文本;
$\text{IndCo}(s)$越小:越像是随机字符串。
按照这个方法,我们就可以区分这两种不同频率分布的字符串。
思路:对某一个密钥长度 $k$ ,我们可以计算出每一个子字符串的 $\text{IndCo}(s_i)$,然后取平均值,如果平均值大于0.06,那么很大概率上这个 $k$ 就是正确的密钥长度。
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
from string import ascii_lowercase as alphabet
def IndCo(s):
'''
Index of Coincidence.
:param str s: The Substring.
:return: The index of coincidence of the substring.
:rtype: float
'''
N = len(s)
frequency = [s.count(c) for c in alphabet]
return sum(i**2 - i for i in frequency) / (N**2 - N)
def CalKeyLength(s):
'''
Calculate the probable key lengths using the index of coincidence method.
:param str s: The character string to be analysed.
:return: All the probable key lengths.
:rtype: list
'''
res = []
for kl in range(2, 100): # Key length range can be adjusted accordingly.
subs = [s[i::kl] for i in range(kl)] # Group into substrings.
if sum(IndCo(si) for si in subs) / kl > 0.06:
if all(map(lambda x: kl % x, res)): # Avoid multiples.
res.append(kl)
return res
|
现在假设我们已经通过上述的两种方法获取了密钥长度,为 $k$ 。
接下来,就只需确定出 $k$ 组凯撒(移位)密码的偏移量,即可恢复keyword,解出明文。
问题是:如何确定每一组的偏移量?
如果给我们的密文序列足够长的话,那么基本上每一组子字符串都会呈现出十分明显的频率分布特征。也就是说,在子字符串中出现次数最多的密文字母,很大概率上对应的就是出现次数最多的字母,即字母e。
而这就足以让我们能够算出偏移量:偏移量 = 出现次数最多的密文字母 - 字母e (mod 26)
例如:在某一组子字符串中出现次数最多的密文字母为h,那么这一组对应的偏移量即为
$$
7 - 4 \equiv 3 \quad (\text{mod}\ 26)
$$
这样,我们可以算出每一组字符串的偏移量,进而恢复出keyword,最后解密。
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
def RecoverKeyword_1(ct, kl):
'''
Recover the keyword according to the most frequent letters.
:param str ct: The ciphertext.
:param int kl: The key length.
:return: The recovered keyword.
:rtype: str
'''
keyword = ''
subs = [ct[i::kl] for i in range(kl)]
for s in subs:
frequency = [s.count(c) for c in alphabet]
most_fqc = max(frequency)
keyword += alphabet[(frequency.index(most_fqc) - 4) % len(alphabet)]
return keyword
|
上面这个方法是建立在密文序列足够长的情况下,才会使得每一组子字符串中出现次数最多的字母全都是e。但是,有些时候,给我们的密文序列并不够长,每一组子字符串中出现次数最多的字母很可能不是e,有可能会是t, a, o, etc.,这个时候上面这个方法就不太适用了。
下面我们给出一个统计学方法Chi-squared Statistic:
Chi-squared Statistic是一个用来衡量两类概率分布的相似程度的统计方法。如果这两类分布完全相同,那么chi-squared statistic为0,如果这两类分布十分不同,那么就会得到比较高的结果。
Chi-squared Statistic定义如下:
$$
\chi^2(C, E) = \sum_{i=0}^{i=25} \frac{(C_i - E_i)^2}{E_i}
$$
其中 $C_i$ 是数字 $i$ 对应字母的出现个数,$E_i$ 是对应字母期望的出现个数。
思路:我们可以对每一组子字符串尝试所有可能的偏移量(总共26种可能)去解密,然后用Chi-squared Statistic来衡量解密后的字符串和普通英文文本的频率分布的相似程度,Chi-squared Statistic最小值所对应的偏移量就应当是正确的偏移量。
e.g.
对于一组用凯撒密码(同一个偏移量)加密的密文:
aoljhlzhyjpwolypzvulvmaollhysplzaruvduhukzptwslzajpwoly
zpapzhafwlvmzbizapabapvujpwolypudopjolhjoslaalypuaolwsh
pualeapzzopmalkhjlyahpuubtilyvmwshjlzkvduaolhswohila
总共有162个字母,根据wiki上的字母频率表
,
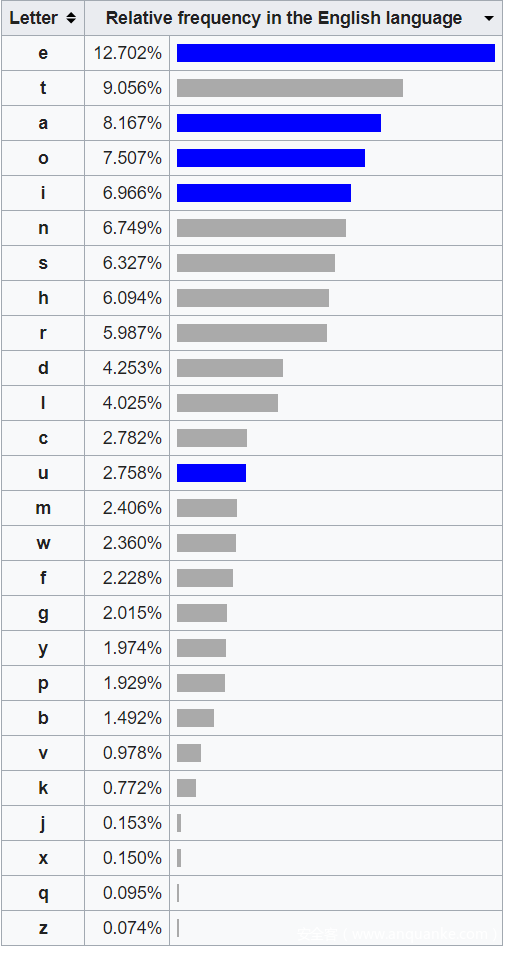
我们可以知道,字母e期望的个数应当为 $162 \times 0.12702 = 20.57724$;字母t期望的个数应当为 $162 \times 0.09056 = $14.67072;依此类推,可以计算出每一个字母期望的个数。
假设尝试的偏移量为10,我们来计算一下这个偏移量所对应的Chi-squared Statistic:
用偏移量10解密密文,得到可能的明文如下:
qebzxbpxozfmebofplkblcqebbxoifbpqhkltkxkapfjmibpqzfmebo
pfqfpxqvmblcprypqfqrqflkzfmebofktefzebxzeibqqbofkqebmix
fkqbuqfppefcqbaxzboqxfkkrjybolcmixzbpaltkqebximexybq
字母e在可能的明文中出现的次数为12,计算得
$$
\frac{(C_4 - E_4)^2}{E_4} = \frac{(12 - 20.57724)^2}{20.57724} = 3.57526.
$$
字母t在可能的明文中出现的次数为3,计算得
$$
\frac{(C_{19} - E_{19})^2}{E_{19}} = \frac{(3 - 14.67072)^2}{14.67072} = 9.28419.
$$
依次计算出其他24个字母的 $\frac{(C_i - E_i)^2}{E_i}$,然后求和,得到3557.93,即为这个偏移量所对应的Chi-squared Statistic。
然后继续穷举剩余的25个偏移量,分别计算出Chi-squared Statistic:
shift plaintext chi-squared
-----------------------------------------------------
0 aoljhlzhyjpwolypzvul... 1631.14
1 znkigkygxiovnkxoyutk... 3435.58
2 ymjhfjxfwhnumjwnxtsj... 2970.75
3 xligeiwevgmtlivmwsri... 1546.41
4 wkhfdhvduflskhulvrqh... 1194.14
5 vjgecguctekrjgtkuqpg... 1461.07
6 uifdbftbsdjqifsjtpof... 1818.22
7 thecaesarcipherisone... 30.71
8 sgdbzdrzqbhogdqhrnmd... 1759.97
9 rfcaycqypagnfcpgqmlc... 1383.66
10 qebzxbpxozfmebofplkb... 3557.93
11 pdaywaownyeldaneokja... 808.44
12 oczxvznvmxdkczmdnjiz... 4641.41
13 nbywuymulwcjbylcmihy... 760.08
14 maxvtxltkvbiaxkblhgx... 2237.19
15 lzwuswksjuahzwjakgfw... 1781.72
16 kyvtrvjritzgyvizjfev... 3521.91
17 jxusquiqhsyfxuhyiedu... 2972.49
18 iwtrpthpgrxewtgxhdct... 1364.30
19 hvsqosgofqwdvsfwgcbs... 958.50
20 gurpnrfnepvcurevfbar... 469.77
21 ftqomqemdoubtqdueazq... 4408.58
22 espnlpdlcntaspctdzyp... 697.88
23 dromkockbmszrobscyxo... 1239.69
24 cqnljnbjalryqnarbxwn... 1853.82
25 bpmkimaizkqxpmzqawvm... 3027.01
可以看到,chi-squared最小的那一行,30.71,对应的即为正确的偏移量和明文。
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
from string import ascii_lowercase as alphabet
LETTER_FREQUENCY = { # From https://en.wikipedia.org/wiki/Letter_frequency.
'e': 0.12702,
't': 0.09056,
'a': 0.08167,
'o': 0.07507,
'i': 0.06966,
'n': 0.06749,
's': 0.06327,
'h': 0.06094,
'r': 0.05987,
'd': 0.04253,
'l': 0.04025,
'c': 0.02782,
'u': 0.02758,
'm': 0.02406,
'w': 0.02360,
'f': 0.02228,
'g': 0.02015,
'y': 0.01974,
'p': 0.01929,
'b': 0.01492,
'v': 0.00978,
'k': 0.00772,
'j': 0.00153,
'x': 0.00150,
'q': 0.00095,
'z': 0.00074
}
def ChiSquared(s):
'''
Calculate the `Chi-squared Statistic`.
:param str s: The string to be analysed.
:return: The `Chi-squared Statistic` of the string.
:rtype: float
'''
f = lambda c: LETTER_FREQUENCY[c] * len(s)
return sum((s.count(c) - f(c))**2 / f(c) for c in alphabet)
def RecoverKeyword_2(ct, kl):
'''
Recover the keyword according to the `Chi-squared Statistic`.
:param str ct: The ciphertext.
:param int kl: The key length.
:return: The recovered keyword.
:rtype: str
'''
keyword = ''
subs = [ct[i::kl] for i in range(kl)]
for s in subs:
chi_squareds = []
for shift in range(len(alphabet)): # Try all possible shifts.
shifted_s = ''.join(\
alphabet[(alphabet.index(c) - shift) % len(alphabet)]\
for c in s)
chi_squareds.append((shift, ChiSquared(shifted_s)))
keyword += alphabet[min(chi_squareds, key=lambda x: x[1])[0]]
return keyword
|
恢复出keyword后,正常解密即可得到明文。
这边,我们用两道CTF里面出现过与Vigenere Cipher相关的密码题,来展示上述方法在实际运用中的效果。
- 2019 西湖论剑线下赛 VVVV
- 2019 De1CTF xorz
题目的源文件及exp,已经上传至Mega
。
encrypt.py文件主要内容如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
# ...
cton = lambda x: ord(x) - ord('a')
ntoc = lambda x: chr(x + ord('a'))
ret = ""
for k, v in enumerate(content):
v = string.lower(v)
if v in "{}":ret += v
if not v in string.ascii_lowercase:
continue
s = secret[k % len(secret)]
ret += ntoc( (cton(v) + cton(s)) % 26)
open("cipher", "w").write(ret)
|
简单的代码审计之后,可以发现这就是一个常规的Vigenere Cipher。
cipher文件中有大概25W+个字母,在文件的结尾能看到:
这一段内容很像是flag。
按照流程,先判断密钥长度,再恢复keyword。
使用The Index of Coincidence方法,可以得出密钥长度:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
from string import ascii_lowercase as alphabet
def IndCo(s):
N = len(s)
frequency = [s.count(c) for c in alphabet]
return sum(i**2 - i for i in frequency) / (N**2 - N)
def CalKeyLength(s):
res = []
for kl in range(2, 100):
subs = [s[i::kl] for i in range(kl)]
if sum(IndCo(si) for si in subs) / kl > 0.06:
if all(map(lambda x: kl % x, res)):
res.append(kl)
return res
with open('cipher', 'r') as f:
cipher = f.read()
print(CalKeyLength(cipher))
# output: [21]
|
得到密钥长度为21。
由于cipher序列的长度足够长,我们可以仅找出频率最高的字母,减去e,即可得到偏移量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
# continue...
keyLength = 21
def RecoverKeyword_1(ct, kl):
keyword = ''
subs = [ct[i::kl] for i in range(kl)]
for s in subs:
frequency = [s.count(c) for c in alphabet]
most_fqc = max(frequency)
keyword += alphabet[(frequency.index(most_fqc) - 4) % len(alphabet)]
return keyword
print(RecoverKeyword_1(cipher, keyLength))
# output: fnxtldpznxpzprdlppdzn
|
成功得到keyword = 'fnxtldpznxpzprdlppdzn'。
用Chi-squared Statistic,也能得到同样的结果,只不过慢了一点。
最后解密即可。
Note:cipher末尾有'{'和'}',用Encryption & Decryption里的解密代码会有问题,需要进行一些修改才行。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
# continue...
from itertools import cycle
keyword = 'fnxtldpznxpzprdlppdzn'
def Vigenere_dec(ct, k):
shifts = cycle(alphabet.index(c) for c in k)
pt = ''
for c in ct.lower():
if c not in alphabet:
next(shifts)
pt += c
continue
pt += alphabet[(alphabet.index(c) - next(shifts)) % len(alphabet)]
return pt
plain = Vigenere_dec(cipher, keyword)
print(plain[-50:])
# output: hewouldnotlethiminthedoorflag{thisistheflagtakeit}
|
最终得到flag{thisistheflagtakeit}。
明文好像是一段马尔克斯的生平传记。
完整exp:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
from itertools import cycle
from string import ascii_lowercase as alphabet
def IndCo(s):
N = len(s)
frequency = [s.count(c) for c in alphabet]
return sum(i**2 - i for i in frequency) / (N**2 - N)
def CalKeyLength(s):
res = []
for kl in range(2, 100):
subs = [s[i::kl] for i in range(kl)]
if sum(IndCo(si) for si in subs) / kl > 0.06:
if all(map(lambda x: kl % x, res)):
res.append(kl)
return res
def RecoverKeyword_1(ct, kl):
keyword = ''
subs = [ct[i::kl] for i in range(kl)]
for s in subs:
frequency = [s.count(c) for c in alphabet]
most_fqc = max(frequency)
keyword += alphabet[(frequency.index(most_fqc) - 4) % len(alphabet)]
return keyword
def Vigenere_dec(ct, k):
shifts = cycle(alphabet.index(c) for c in k)
pt = ''
for c in ct.lower():
if c not in alphabet:
next(shifts)
pt += c
continue
pt += alphabet[(alphabet.index(c) - next(shifts)) % len(alphabet)]
return pt
def main():
with open('cipher', 'r') as f:
cipher = f.read()
keyLengths = CalKeyLength(cipher)
print(f"All the probable key lengths: {keyLengths}")
for kl in keyLengths:
keyword = RecoverKeyword_1(cipher, kl)
print(f"keyword: {keyword}")
plain = Vigenere_dec(cipher, keyword)
print(plain[-50:])
if __name__ == '__main__':
main()
|
crypto_xorz.py文件内容如下:
1
2
3
4
5
6
7
8
9
10
11
12
|
from itertools import *
from data import flag,plain
key=flag.strip("de1ctf{").strip("}")
assert(len(key)<38)
salt="WeAreDe1taTeam"
ki=cycle(key)
si=cycle(salt)
cipher = ''.join([hex(ord(p) ^ ord(next(ki)) ^ ord(next(si)))[2:].zfill(2) for p in plain])
print cipher
# output:
# 49380d773440222d1b421b3060380c3f403c3844791b202651306721135b6229294a3c3222357e766b2f15561b35305e3c3b670e49382c295c6c170553577d3a2b791470406318315d753f03637f2b614a4f2e1c4f21027e227a4122757b446037786a7b0e37635024246d60136f7802543e4d36265c3e035a725c6322700d626b345d1d6464283a016f35714d434124281b607d315f66212d671428026a4f4f79657e34153f3467097e4e135f187a21767f02125b375563517a3742597b6c394e78742c4a725069606576777c314429264f6e330d7530453f22537f5e3034560d22146831456b1b72725f30676d0d5c71617d48753e26667e2f7a334c731c22630a242c7140457a42324629064441036c7e646208630e745531436b7c51743a36674c4f352a5575407b767a5c747176016c0676386e403a2b42356a727a04662b4446375f36265f3f124b724c6e346544706277641025063420016629225b43432428036f29341a2338627c47650b264c477c653a67043e6766152a485c7f33617264780656537e5468143f305f4537722352303c3d4379043d69797e6f3922527b24536e310d653d4c33696c635474637d0326516f745e610d773340306621105a7361654e3e392970687c2e335f3015677d4b3a724a4659767c2f5b7c16055a126820306c14315d6b59224a27311f747f336f4d5974321a22507b22705a226c6d446a37375761423a2b5c29247163046d7e47032244377508300751727126326f117f7a38670c2b23203d4f27046a5c5e1532601126292f577776606f0c6d0126474b2a73737a41316362146e581d7c1228717664091c
|
代码审计后,发现这是一个修改过的Vigenere Cipher。主要是不使用字母的移位来加密,而是采用了异或的方式,将密文空间从26个字母扩展到了一个字节。也就是说,alphabet变成为0~256。
首先,salt已知,可以异或回去,消除掉salt的效果。
1
2
3
4
5
6
7
|
from itertools import *
salt="WeAreDe1taTeam"
si=cycle(salt)
cipher = bytes.fromhex('49380d773440222d1b421b3060380c3f403c3844791b202651306721135b6229294a3c3222357e766b2f15561b35305e3c3b670e49382c295c6c170553577d3a2b791470406318315d753f03637f2b614a4f2e1c4f21027e227a4122757b446037786a7b0e37635024246d60136f7802543e4d36265c3e035a725c6322700d626b345d1d6464283a016f35714d434124281b607d315f66212d671428026a4f4f79657e34153f3467097e4e135f187a21767f02125b375563517a3742597b6c394e78742c4a725069606576777c314429264f6e330d7530453f22537f5e3034560d22146831456b1b72725f30676d0d5c71617d48753e26667e2f7a334c731c22630a242c7140457a42324629064441036c7e646208630e745531436b7c51743a36674c4f352a5575407b767a5c747176016c0676386e403a2b42356a727a04662b4446375f36265f3f124b724c6e346544706277641025063420016629225b43432428036f29341a2338627c47650b264c477c653a67043e6766152a485c7f33617264780656537e5468143f305f4537722352303c3d4379043d69797e6f3922527b24536e310d653d4c33696c635474637d0326516f745e610d773340306621105a7361654e3e392970687c2e335f3015677d4b3a724a4659767c2f5b7c16055a126820306c14315d6b59224a27311f747f336f4d5974321a22507b22705a226c6d446a37375761423a2b5c29247163046d7e47032244377508300751727126326f117f7a38670c2b23203d4f27046a5c5e1532601126292f577776606f0c6d0126474b2a73737a41316362146e581d7c1228717664091c')
cipher = b''.join(bytes([c ^ ord(next(si))]) for c in cipher)
|
虽然alphabet改变了,但明文应该依旧是普通的英文文本,我们的index of coincidence仍然适用。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
alphabet = list(range(256))
def IndCo(s):
N = len(s)
frequency = [s.count(c) for c in alphabet]
return sum(i**2 - i for i in frequency) / (N**2 - N)
def CalKeyLength(s):
res = []
for kl in range(2, 38):
subs = [s[i::kl] for i in range(kl)]
if sum(IndCo(si) for si in subs) / kl > 0.06:
if all(map(lambda x: kl % x, res)):
res.append(kl)
return res
print(CalKeyLength(cipher))
# output: [30]
|
得到密钥长度为30,接下来是恢复key。
我们先把cipher分成30组:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
kl = 30
subs = [cipher[i::kl] for i in range(kl)]
for s in subs:
print(s)
# output:
# b'\x1e#6$.2:90$9?w292??%#'
# b'][\x13\x13\x13DZV\x13GE\x13]\x13T\x13V\x13\x13\x13'
# b'LL\x18\x01\x08L\x02L\x18\t\x05\x18\x03\x03L\x00\r\x18%\x01'
# b'\x05\x0e\x0b\x1a\x06\n\x06\x07\x0cO\x17\x0b\x11\r\x17\n\x11\x0cC\x02'
# b'QY_\x10CC\x10U\x10\x10UU\x10UX[D\x10S['
# b'\x04\x03\x18\x05\x1dM\x08\x01\x0f\x03\t\x08\x00M\x08\x08\r\x0f\x02\x08'
# b'GV@VZCRZR\\g\x13JUV]@VF@'
# b'\x1cT\x15\x15\x07\x18\x06\x13\x07\x06\x1b\x15T\x1bX\x11TZ\x1aT'
# b'o*!=**<\'*oo#) \x18<<\x00;"'
# b'#\x13\x0e\x1eF\x0bJ\x1eJ\x19\x0b\x05\x03\x06\x02\x19\x06\x04J\x0f'
# b'O\nOO8\x1c\x18\n\x1b\x02\x01\x01\x19\x06\x00O\x0e\x03\x02O'
# b'UBTEYTXU^THTTB\x11^GHHB'
# b'\x01B\x1c\x06\x01\n\x1aU\x1b\x02N@N\x06\x02\x08\x0bNN\x07'
# b'U3\x07\x14UU\x1d;\x16\x19\x067\x06U\x10UU\x18\x12\x1b'
# b'[ZZA\\A\x15Z]\x19P@P]TTTLT\x15'
# b'ZGG\x15[ZAGP\x15[A[PC\x15[\x15\\T'
# b'\x01U\x06\x19UU\x1dU\x06\x11\x06U\x06\x14\x10\x18\x11\x05\x1b\x02'
# b'N\x1aN\x01\n\n\x17\x1aN\x0b\x1b\x03\x0b\x1c\x1d\x0fN\x02B\x0f'
# b']Y_GT^\x11TABPHBE\x11_GPeC'
# b'\x00\n\x00\n\x1c\x1b\x1b\x01\x1d\x06\x03OOO\x1aC\x0e\x08\x07\x0b'
# b'\x1c\x13\x1e\x19\x1a\x0f\x05\x0e\x05\x18J\x0c\t\x0c\x04>\x19\x1f\x0b\x19'
# b"*o*o&a!*!*)&.=<'<*;o"
# b'T\x1dO\x03\x00:\x13\x06\x11T\x11\x02\x1a\x1b\x03\r\x15TT\x19'
# b'G]q[V\\F\x13\x1fGRVw^R\x13_G@V'
# b'\x05M\x18\x0cM\x1f\x08\x0b#\x02\x1eM\x04M\x14\x1dM\x05\x05M'
# b'UDDD_\x10PU_\x10DGCCUBGEU@'
# b'\x06\x0bCC\x05\x02\x10\x06\x11\x01C\n\x10\x06\x07\x0c\x11\x10C\x02'
# b'L\t\x0c\x18L\x1eL\x00L\t\x1b\x18\x19\x1eL\x19\tL\x18\x05'
# b'DVG[EVGZG\x13Z@REGWGU[]'
# b'>w>2>w"96>#{3>?w466y'
|
对每一组子字节序列,我们仍然可以尝试所有256种可能的异或值。
明文空间可能不止小写字母(还可能有空格、符号、大写字母),使用Chi-squared Statistic方法,效果不太理想。
我们可以换一个方案:按字母的出现的概率对整个字符串进行评分,每一次尝试解密的结果中每有一个字母就加上对应的权重分,评分越高就说明这个结果越像是普通的英文文本。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
# continue...
LETTER_FREQUENCY = {...}
def score(s):
score = 0
for c in s.lower():
if c in LETTER_FREQUENCY:
score += LETTER_FREQUENCY[c]
return score
def RecoverKey(ct, kl):
key = b''
subs = [ct[i::kl] for i in range(kl)]
for s in subs:
scores = []
for xor in range(256): # Try all possible xor values.
xored_s = ''.join(chr(c ^ xor) for c in s)
scores.append((xor, score(xored_s)))
key += bytes([max(scores, key=lambda x: x[1])[0]])
return key
kl = 30
key = RecoverKey(cipher, kl)
print(key)
print(Vigenere_dec(cipher, key))
# output:
# b'Wvlc0m3tOjo1nu55un1ojOt3q0cl3W'
# I+ faith I do not love ttee wit- mine eyes,For they in<thee aethousand errors note;Bit `tisemy heart that loves wh}t theyedespise,Who in despite<of vie2 is pleased to dote.Non are m,ne ears with thy tonguy`s tun delighted;Nor tender zeelingeto base touches prone,Ror tas1e, nor smell, desire ts be in3itedTo any sensual feaot withethee alone.But my five<wits, +or my five senses canDussuadeeone foolish heart from<servin" thee,Who leaves unswaeed theelikeness of a man,Thy lroud h art`s slave and vassal<wretcheto be.Only my plague ttus fareI count my gain,That ste thatemakes me sin awards me<pain.
|
可以看到,key和明文虽然有个别不太正常,基本上已经很明显了。
如果再仔细观察一下key,能够发现实际上key是一个回文字符串,可以恢复出正确的key:W3lc0m3tOjo1nu55un1ojOt3m0cl3W。
再去解密,能够得到完整的明文:
In faith I do not love thee with mine eyes,For they in thee a thousand errors note;But `tis my heart that loves what they despise,Who in despite of view is pleased to dote.Nor are mine ears with thy tongue`s tune delighted;Nor tender feeling to base touches prone,Nor taste, nor smell, desire to be invitedTo any sensual feast with thee alone.But my five wits, nor my five senses canDissuade one foolish heart from serving thee,Who leaves unswayed the likeness of a man,Thy proud heart`s slave and vassal wretch to be.Only my plague thus far I count my gain,That she that makes me sin awards me pain.
事实上,如果明文是带有空格的话(虽然也有大写字母和符号,但基本可以不用考虑),我们在计算LETTER_FREQUENCY的时候是要把空格放进去考虑的。一般来说,空格出现的次数大概是字母e的两倍,所以我们可以在LETTER_FREQUENCY中加入一个' '键,值为0.25000。再去恢复key,就能够十分精准地解出W3lc0m3tOjo1nu55un1ojOt3m0cl3W。
最终exp:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
|
from itertools import *
from string import printable
alphabet = list(range(256))
LETTER_FREQUENCY = {
' ': 0.25000,
'e': 0.12702,
't': 0.09056,
'a': 0.08167,
'o': 0.07507,
'i': 0.06966,
'n': 0.06749,
's': 0.06327,
'h': 0.06094,
'r': 0.05987,
'd': 0.04253,
'l': 0.04025,
'c': 0.02782,
'u': 0.02758,
'm': 0.02406,
'w': 0.02360,
'f': 0.02228,
'g': 0.02015,
'y': 0.01974,
'p': 0.01929,
'b': 0.01492,
'v': 0.00978,
'k': 0.00772,
'j': 0.00153,
'x': 0.00150,
'q': 0.00095,
'z': 0.00074
}
def IndCo(s):
N = len(s)
frequency = [s.count(c) for c in alphabet]
return sum(i**2 - i for i in frequency) / (N**2 - N)
def CalKeyLength(s):
res = []
for kl in range(2, 38):
subs = [s[i::kl] for i in range(kl)]
if sum(IndCo(si) for si in subs) / kl > 0.06:
if all(map(lambda x: kl % x, res)):
res.append(kl)
return res
def score(s):
score = 0
for c in s.lower():
if c in LETTER_FREQUENCY:
score += LETTER_FREQUENCY[c]
return score
def RecoverKey(ct, kl):
key = b''
subs = [ct[i::kl] for i in range(kl)]
for s in subs:
scores = []
for xor in range(256):
xored_s = ''.join(chr(c ^ xor) for c in s)
if all(c in printable for c in xored_s):
scores.append((xor, score(xored_s)))
key += bytes([max(scores, key=lambda x: x[1])[0]])
return key
def Vigenere_dec(cipher, key):
keyCircle = cycle(key)
pt = ''
for c in cipher:
pt += chr(c ^ next(keyCircle))
return pt
def main():
salt="WeAreDe1taTeam"
si=cycle(salt)
cipher = bytes.fromhex('49380d773440222d1b421b3060380c3f403c3844791b202651306721135b6229294a3c3222357e766b2f15561b35305e3c3b670e49382c295c6c170553577d3a2b791470406318315d753f03637f2b614a4f2e1c4f21027e227a4122757b446037786a7b0e37635024246d60136f7802543e4d36265c3e035a725c6322700d626b345d1d6464283a016f35714d434124281b607d315f66212d671428026a4f4f79657e34153f3467097e4e135f187a21767f02125b375563517a3742597b6c394e78742c4a725069606576777c314429264f6e330d7530453f22537f5e3034560d22146831456b1b72725f30676d0d5c71617d48753e26667e2f7a334c731c22630a242c7140457a42324629064441036c7e646208630e745531436b7c51743a36674c4f352a5575407b767a5c747176016c0676386e403a2b42356a727a04662b4446375f36265f3f124b724c6e346544706277641025063420016629225b43432428036f29341a2338627c47650b264c477c653a67043e6766152a485c7f33617264780656537e5468143f305f4537722352303c3d4379043d69797e6f3922527b24536e310d653d4c33696c635474637d0326516f745e610d773340306621105a7361654e3e392970687c2e335f3015677d4b3a724a4659767c2f5b7c16055a126820306c14315d6b59224a27311f747f336f4d5974321a22507b22705a226c6d446a37375761423a2b5c29247163046d7e47032244377508300751727126326f117f7a38670c2b23203d4f27046a5c5e1532601126292f577776606f0c6d0126474b2a73737a41316362146e581d7c1228717664091c')
cipher = b''.join(bytes([c ^ ord(next(si))]) for c in cipher)
kls = CalKeyLength(cipher)
print(f"All probable key length: {kls}")
for kl in kls:
key = RecoverKey(cipher, kl)
print(f"Key: {key}")
print(Vigenere_dec(cipher, key))
if __name__ == '__main__':
main()
|
flag:de1ctf{W3lc0m3tOjo1nu55un1ojOt3m0cl3W}
另有一篇也是介绍这种异或运算的变种Vigenere Cipher的文章:小记一类ctf密码题解题思路
。解这道题的时候从中借鉴了一些思路,有兴趣的可以去看看。
An Introduction to Mathematical Cryptography
Letter frequency - Wikipedia
Vigenere Cipher - Practical Cryptography
Chi-squared Statistic - Practical Cryptography
小记一类ctf密码题解题思路